Single degree of freedom spring-slider system¶

(P333, Segal 2010)

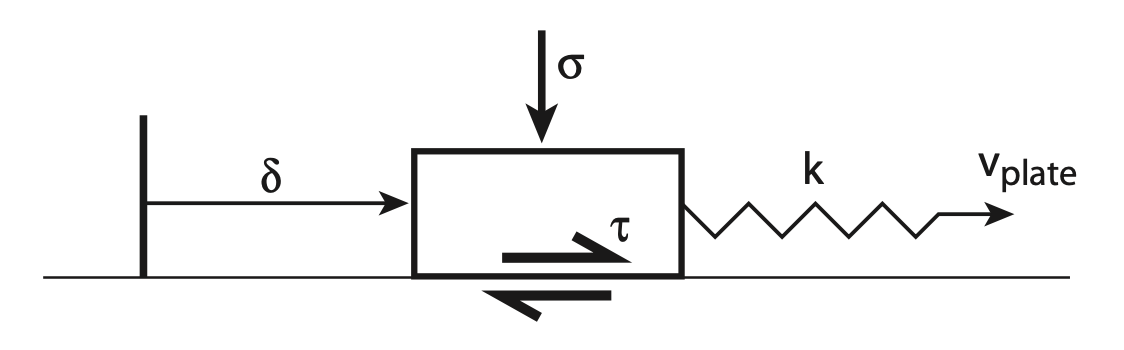
\begin{align} \tau &=\tau_0 - n V - \kappa \delta \\ η &= \frac{\mu}{2c} \\ \kappa &= \frac{2\mu}{\pi L} \\ \end{align}

$$ \tau_{lock} = \tau_0 - \kappa \delta \\ $$ $$ \tau_{str}(\delta)= \begin{cases}\tau_p-\left(\tau_p-\tau_r\right) \delta / D_c, & \delta \le D_c \\ \tau_r & \delta>D_c\end{cases} $$

\begin{align} f &= f_s - (f_s - f_d) * \min(\delta, D_c) / D_c \nonumber \\ \tau_{str} &= f \cdot σ_n \nonumber \end{align}

In [1]:

import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display, clear_output

import numpy as np import matplotlib.pyplot as plt from IPython.display import display, clear_output

In [2]:

L = 1                   #fault length (m)
μ = 30e3                #shear modulus (MPa)
c = 3e3                 #shear wave speed (m/s)
π = np.pi
κ = 2.0 * μ / (π * L)   #stiffness (MPa/m)
η = 0.5 * μ / c         #radiation-damping coefficient

L = 1 #fault length (m) μ = 30e3 #shear modulus (MPa) c = 3e3 #shear wave speed (m/s) π = np.pi κ = 2.0 * μ / (π * L) #stiffness (MPa/m) η = 0.5 * μ / c #radiation-damping coefficient

In [3]:

fs = 0.8        #static friction coefficient
fd = 0.7        #dynamic friction coefficient
Dc = 10e-6      #slip weakening distance (m)

fs = 0.8 #static friction coefficient fd = 0.7 #dynamic friction coefficient Dc = 10e-6 #slip weakening distance (m)

In [4]:

σn = 100.0      #effective normal stress (MPa)
τ0 = fs * σn    #initial shear stress (MPa)
dτdt = 1e-6     #shear stress rate (MPa/s)

σn = 100.0 #effective normal stress (MPa) τ0 = fs * σn #initial shear stress (MPa) dτdt = 1e-6 #shear stress rate (MPa/s)

In [5]:

δ = np.linspace(0, 2 * Dc, 100)                 #slip (m)
f = fs - (fs - fd) * np.minimum(δ, Dc) / Dc     #slip-weakening friction
τ_str = f * σn                                  #fault strength (MPa)

δ = np.linspace(0, 2 * Dc, 100) #slip (m) f = fs - (fs - fd) * np.minimum(δ, Dc) / Dc #slip-weakening friction τ_str = f * σn #fault strength (MPa)

In [6]:

plt.figure()
plt.plot(δ, τ_str)
plt.vlines(Dc, 0, fd * σn, linestyle="--", label="Dc")
plt.legend()
plt.ylim(60)
plt.xlabel("Slip-weakening distance (δ)")
plt.ylabel("Fault strength (τ_str)")

plt.figure() plt.plot(δ, τ_str) plt.vlines(Dc, 0, fd * σn, linestyle="--", label="Dc") plt.legend() plt.ylim(60) plt.xlabel("Slip-weakening distance (δ)") plt.ylabel("Fault strength (τ_str)")

Out[6]:

Text(0, 0.5, 'Fault strength (τ_str)')

In [7]:

v_max = (fs - fd) * σn / η
τ_min = fd * σn
τ_max = fs * σn
δ_max = (τ_max - τ_min) / κ
t_max = η / κ * 2.0
L_min = 2.0 * μ / π * Dc / (τ_max - τ_min)

nt = 10000
dt = 1e-7

v_max = (fs - fd) * σn / η τ_min = fd * σn τ_max = fs * σn δ_max = (τ_max - τ_min) / κ t_max = η / κ * 2.0 L_min = 2.0 * μ / π * Dc / (τ_max - τ_min) nt = 10000 dt = 1e-7

In [8]:

fig, ax = plt.subplots(3, 2, figsize=(8, 10))
t_hist = []
τ_hist = []
v_hist = []
δ_hist = []

δ = 0
for i in range(nt):

    τ0 += dτdt * dt
    Δτ = -κ * δ
    τ_lock = τ0 + Δτ

    f = fs - (fs - fd) * min(δ, Dc) / Dc
    τ_str = f * σn

    if τ_lock < τ_str:
        τ = τ_lock
        v = 0
    else:
        τ = τ_str
        v = -(τ_str - τ_lock) / η

    δ = δ + dt * v
    t_hist.append(i * dt)
    τ_hist.append(τ)
    v_hist.append(v)
    δ_hist.append(δ)

    if i % 100 == 0:
        [axi.clear() for axi in ax.ravel()]
        ax[0, 0].plot(t_hist, v_hist, lw=2)
        ax[0, 1].plot(t_hist, v_hist, lw=2)
        ax[0, 1].set_ylim(0, v_max)
        ax[0, 1].set_title("Fixed ylim")
        ax[0, 0].set_ylabel("Velocity (v)")
        ax[1, 0].plot(t_hist, τ_hist, lw=2)
        ax[1, 1].plot(t_hist, τ_hist, lw=2)
        ax[1, 1].set_ylim(τ_min, τ_max)
        ax[1, 0].set_ylabel("Fault stength (τ)")
        ax[2, 0].plot(t_hist, δ_hist, lw=2)
        ax[2, 1].plot(t_hist, δ_hist, lw=2)
        ax[2, 1].set_ylim(0, δ_max)
        ax[2, 0].set_ylabel("Slip (δ)")
        ax[2, 1].ticklabel_format(style="sci", axis="y", scilimits=(0, 0))
        [axi.ticklabel_format(style="sci", axis="x", scilimits=(0, 0)) for axi in ax.ravel()]
        ax[2, 0].set_xlabel("Time (s)")
        ax[2, 1].set_xlabel("Time (s)")
        
        display(fig)
        clear_output(wait=True)

fig, ax = plt.subplots(3, 2, figsize=(8, 10)) t_hist = [] τ_hist = [] v_hist = [] δ_hist = [] δ = 0 for i in range(nt): τ0 += dτdt * dt Δτ = -κ * δ τ_lock = τ0 + Δτ f = fs - (fs - fd) * min(δ, Dc) / Dc τ_str = f * σn if τ_lock < τ_str: τ = τ_lock v = 0 else: τ = τ_str v = -(τ_str - τ_lock) / η δ = δ + dt * v t_hist.append(i * dt) τ_hist.append(τ) v_hist.append(v) δ_hist.append(δ) if i % 100 == 0: [axi.clear() for axi in ax.ravel()] ax[0, 0].plot(t_hist, v_hist, lw=2) ax[0, 1].plot(t_hist, v_hist, lw=2) ax[0, 1].set_ylim(0, v_max) ax[0, 1].set_title("Fixed ylim") ax[0, 0].set_ylabel("Velocity (v)") ax[1, 0].plot(t_hist, τ_hist, lw=2) ax[1, 1].plot(t_hist, τ_hist, lw=2) ax[1, 1].set_ylim(τ_min, τ_max) ax[1, 0].set_ylabel("Fault stength (τ)") ax[2, 0].plot(t_hist, δ_hist, lw=2) ax[2, 1].plot(t_hist, δ_hist, lw=2) ax[2, 1].set_ylim(0, δ_max) ax[2, 0].set_ylabel("Slip (δ)") ax[2, 1].ticklabel_format(style="sci", axis="y", scilimits=(0, 0)) [axi.ticklabel_format(style="sci", axis="x", scilimits=(0, 0)) for axi in ax.ravel()] ax[2, 0].set_xlabel("Time (s)") ax[2, 1].set_xlabel("Time (s)") display(fig) clear_output(wait=True)