import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import pandas as pd
Classifying volcanic rocks¶
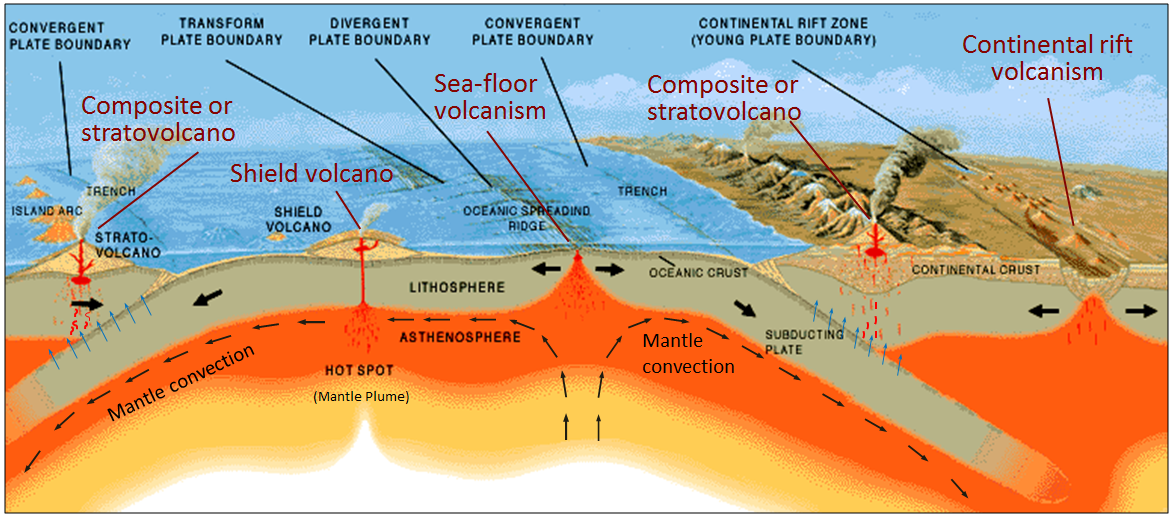
Today we will continue to deal with igneous geochemistry data. Igneous rocks are those that crystallize from cooling magma. Different magmas have different compositions associated with their origin as we explored a week ago. During class today, we will focus on data from mafic lava flows (these are called basalts and are the relatively low silica, high iron end of what we looked at last week).
Igneous rocks form in a wide variety of tectonic settings, including mid-ocean ridges, ocean islands, and volcanic arcs. It is a problem of great interest to igneous petrologists to recover the original tectonic setting of mafic rocks of the past. When the geological setting alone cannot unambiguously resolve this question, the chemical composition of these rocks might contain the answer. The major, minor, and trace elemental composition of basalts shows large variations, for example as a function of formation depth (e.g., Kushiro and Kuno, 1963) --- Vermeesch (2006)
For this analysis, we are going to use a dataset that was compiled in
Vermeesch (2006) Tectonic discrimination of basalts with classification trees, Geochimica et Cosmochimica Acta https://doi.org/10.1016/j.gca.2005.12.016
These data were grouped into 3 categories:
- 256 Island arc basalts (IAB) from the Aeolian, Izu-Bonin, Kermadec, Kurile, Lesser Antilles, Mariana, Scotia, and Tonga arcs.
- 241 Mid-ocean ridge (MORB) samples from the East Pacific Rise, Mid Atlantic Ridge, Indian Ocean, and Juan de Fuca Ridge.
- 259 Ocean-island (OIB) samples from St. Helena, the Canary, Cape Verde, Caroline, Crozet, Hawaii-Emperor, Juan Fernandez, Marquesas, Mascarene, Samoan, and Society islands.
Let's look at the illustration above and determine where each of these settings are within a plate tectonic context
Import data¶
The data are from the supplemental materials of the Vermeesch (2006) paper. The samples are grouped by affinity MORB, OIB, and IAB.
basalt_data = pd.read_csv('data/Vermeesch2006.csv')
basalt_data.tail()
| affinity | SiO2_wt_percent | TiO2_wt_percent | Al2O3_wt_percent | Fe2O3_wt_percent | FeO_wt_percent | CaO_wt_percent | MgO_wt_percent | MnO_wt_percent | K2O_wt_percent | ... | Hf_ppm | Ta_ppm | Pb_ppm | Th_ppm | U_ppm | 143Nd/144Nd | 87Sr/86Sr | 206Pb/204Pb | 207Pb/204Pb | 208Pb/204Pb | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 751 | IAB | 50.97 | 0.78 | 18.86 | NaN | NaN | 10.85 | 4.71 | 0.16 | 0.60 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 18.82 | 15.556 | 38.389 |
| 752 | IAB | 51.00 | 1.41 | 17.06 | 3.80 | 7.04 | 9.97 | 4.96 | 0.17 | 0.73 | ... | NaN | NaN | NaN | NaN | NaN | NaN | 0.70348 | NaN | NaN | NaN |
| 753 | IAB | 52.56 | 1.21 | 17.74 | 2.28 | 7.53 | 10.48 | 5.57 | 0.24 | 0.29 | ... | NaN | NaN | NaN | NaN | NaN | NaN | 0.70362 | NaN | NaN | NaN |
| 754 | IAB | 52.59 | 1.50 | 16.88 | 2.41 | 7.90 | 10.83 | 4.91 | 0.26 | 0.54 | ... | NaN | NaN | NaN | NaN | NaN | NaN | 0.70363 | NaN | NaN | NaN |
| 755 | IAB | 52.96 | 1.27 | 15.65 | 2.91 | 9.32 | 9.78 | 4.24 | 0.23 | 0.46 | ... | NaN | NaN | NaN | NaN | NaN | NaN | 0.70352 | NaN | NaN | NaN |
5 rows × 52 columns
print(basalt_data.columns)
Index(['affinity', 'SiO2_wt_percent', 'TiO2_wt_percent', 'Al2O3_wt_percent',
'Fe2O3_wt_percent', 'FeO_wt_percent', 'CaO_wt_percent',
'MgO_wt_percent', 'MnO_wt_percent', 'K2O_wt_percent', 'Na2O_wt_percent',
'P2O5(wt%)', 'La_ppm', 'Ce_ppm', 'Pr_ppm', 'Nd_ppm', 'Sm_ppm', 'Eu_ppm',
'Gd_ppm', 'Tb_ppm', 'Dy_ppm', 'Ho_ppm', 'Er_ppm', 'Tm_ppm', 'Yb_ppm',
'Lu_ppm', 'Sc_ppm', 'V_ppm', 'Cr_ppm', 'Co_ppm', 'Ni_ppm', 'Cu_ppm',
'Zn_ppm', 'Ga_ppm', 'Rb_ppm', 'Sr_ppm', 'Y_ppm', 'Zr_ppm', 'Nb_ppm',
'Sn_ppm', 'Cs_ppm', 'Ba_ppm', 'Hf_ppm', 'Ta_ppm', 'Pb_ppm', 'Th_ppm',
'U_ppm', '143Nd/144Nd', '87Sr/86Sr', '206Pb/204Pb', '207Pb/204Pb',
'208Pb/204Pb'],
dtype='object')
Can geochemical data be used to classify the tectonic setting?¶
These data are labeled. The author already determined what setting these basalts came from. However, is there are way that we could use these labeled data to determine the setting for an unknown basalt?
A paper published in 1982 proposed that the elements titanium and vanadium were particular good at giving insight into tectonic setting. The details of why are quite complicated and can be summarized as "the depletion of V relative to Ti is a function of the fO2 of the magma and its source, the degree of partial melting, and subsequent fractional crystallization." If you take EPS100B you will learn more about the fundamentals behind this igneous petrology. For the moment, you can consider the working hypothesis behind this classification to that different magmatic environments have differences in oxidation states that are reflected in Ti vs V ratios.
Shervais, J.W. (1982) Ti-V plots and the petrogenesis of modern and ophiolitic lavas Earth and Planetary Science Letters https://doi.org/10.1016/0012-821X(82)90120-0
Plot TiO2 (wt%) vs V (ppm)¶
plt.figure(figsize=(8, 6))
for affinity in basalt_data['affinity'].unique():
subset = basalt_data[basalt_data['affinity'] == affinity]
plt.scatter(subset['TiO2_wt_percent'], subset['V_ppm'], label=affinity, edgecolor='k', s=50)
plt.legend()
plt.xlabel('TiO2 (wt%)')
plt.ylabel('V (ppm)')
plt.show()
Training and testing¶
Import more sklearn tools¶
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.impute import SimpleImputer
Review: Linear logistic regression¶
- Using only $TiO_2$ and V, we can use logistic regression to classify the data into MORB, OIB, and IAB.
## Prepare the data to define the features X and the target y
basalt_data_Ti_V = basalt_data[(~basalt_data['TiO2_wt_percent'].isna()) & (~basalt_data['V_ppm'].isna())]
X = basalt_data_Ti_V[['TiO2_wt_percent', 'V_ppm']].values
y = basalt_data_Ti_V['affinity'].values
## Encode the target variable from string to integer
le = LabelEncoder()
y = le.fit_transform(y)
from sklearn.linear_model import LogisticRegression
## Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Train the model
model = LogisticRegression(solver="liblinear")
model.fit(X_train, y_train)
# Predict the test set
y_pred = model.predict(X_test)
# Calculate the accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
# Confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=le.classes_)
disp.plot(cmap=plt.cm.Blues, values_format='d', colorbar=False);
Accuracy: 0.85
More classification methods¶
Today we will explore a few more classification methods:
- Support vector machines
- Decision trees (Random forests)
- Nearest neighbors
- Neural networks
While there is a nice simplicity to the linear classifier approach comparing the $TiO_2$ vs V data, we have a lot more information from other aspects of the geochemistry. We might as well use that information as well.
Let's use all the data we can.
basalt_data.head(1)
| affinity | SiO2_wt_percent | TiO2_wt_percent | Al2O3_wt_percent | Fe2O3_wt_percent | FeO_wt_percent | CaO_wt_percent | MgO_wt_percent | MnO_wt_percent | K2O_wt_percent | ... | Hf_ppm | Ta_ppm | Pb_ppm | Th_ppm | U_ppm | 143Nd/144Nd | 87Sr/86Sr | 206Pb/204Pb | 207Pb/204Pb | 208Pb/204Pb | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | MORB | 48.2 | 2.52 | 15.2 | 2.31 | 8.56 | 9.69 | 7.15 | 0.17 | 0.9 | ... | 5.2 | NaN | 2.15 | 1.4881 | 0.4941 | NaN | 0.703 | NaN | NaN | NaN |
1 rows × 52 columns
Preparing the data to use features other than TiO2 and V¶
Encode the target variable 'affinity' using LabelEncoder: The target variable 'affinity' contains categorical data, which needs to be encoded as numerical values for the decision tree classifier. The LabelEncoder from scikit-learn is used to transform the 'affinity' column into numerical labels.
Split the data into features (X) and target (y): The dataset is split into two parts, features (X) and the target variable (y). Features are the input variables that the classifier will use to make predictions, and the target variable is the output we want the classifier to predict.
Impute missing values using median imputation: most classifiers cannot handle missing values in the input data. Therefore, missing values in the dataset need to be imputed (filled in) before training the classifier. Let's use median imputation which replaces the missing values with the median of the non-missing values in the same column. We can import and use the
SimpleImputerfunction.
## Prepare the data into features (X) and target (y)
X = basalt_data.drop('affinity', axis=1)
y = basalt_data['affinity']
## We will keep the column names for later use
columns = X.columns
## Encode the target variable
le = LabelEncoder()
y = le.fit_transform(y)
## Impute missing values using median imputation
imputer = SimpleImputer(strategy='median')
X = imputer.fit_transform(X)
## Split the data into training and test sets using 30% of the data for testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=41)
Let's try to apply the same classification methods to the data using all the features.
# Train the model
model = LogisticRegression(solver="liblinear")
model.fit(X_train, y_train)
# Predict the test set
y_pred = model.predict(X_test)
# Calculate the accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
# Confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=le.classes_)
disp.plot(cmap=plt.cm.Blues, values_format='d', colorbar=False);
Accuracy: 0.90
How do the results compare to the linear logistic regression using only TiO2 and V?
Support Vector Machines (SVM)¶
What is a support vector machine?¶
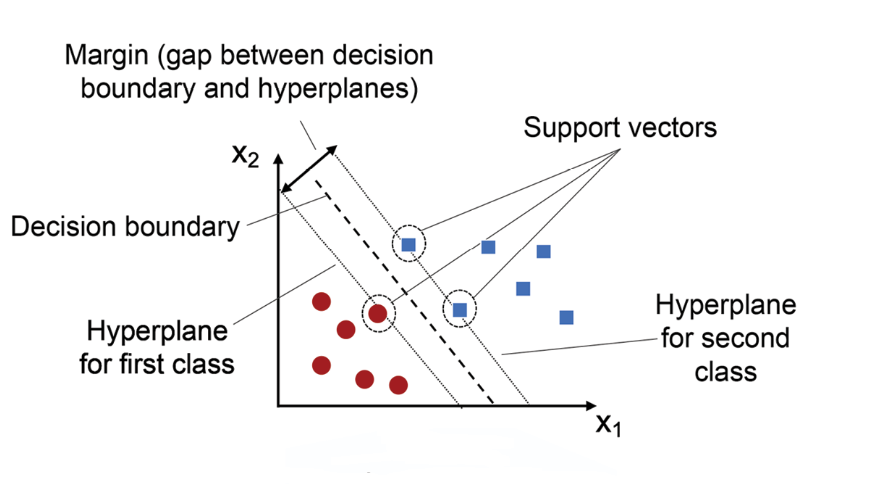
Support vector machines are a type of supervised learning model that can be used for both classification and regression. The basic idea is to find the hyperplane that best separates the classes in the feature space. The hyperplane is defined by the support vectors, which are the points that are closest to the hyperplane. The distance between the support vectors and the hyperplane is called the margin. The goal of the SVM is to maximize the margin, which is done by minimizing the norm of the weight vector. The SVM can be used for both linear and non-linear classification by using different kernel functions.
How does the SVM work?¶
Support vector machines work by finding the hyperplane that best separates the classes in the feature space. The hyperplane is defined by the support vectors, which are the points that are closest to the hyperplane. The distance between the support vectors and the hyperplane is called the margin. The goal of the SVM is to maximize the margin, which is done by minimizing the norm of the weight vector. The SVM can be used for both linear and non-linear classification by using different kernel functions.
What is a kernel function?¶
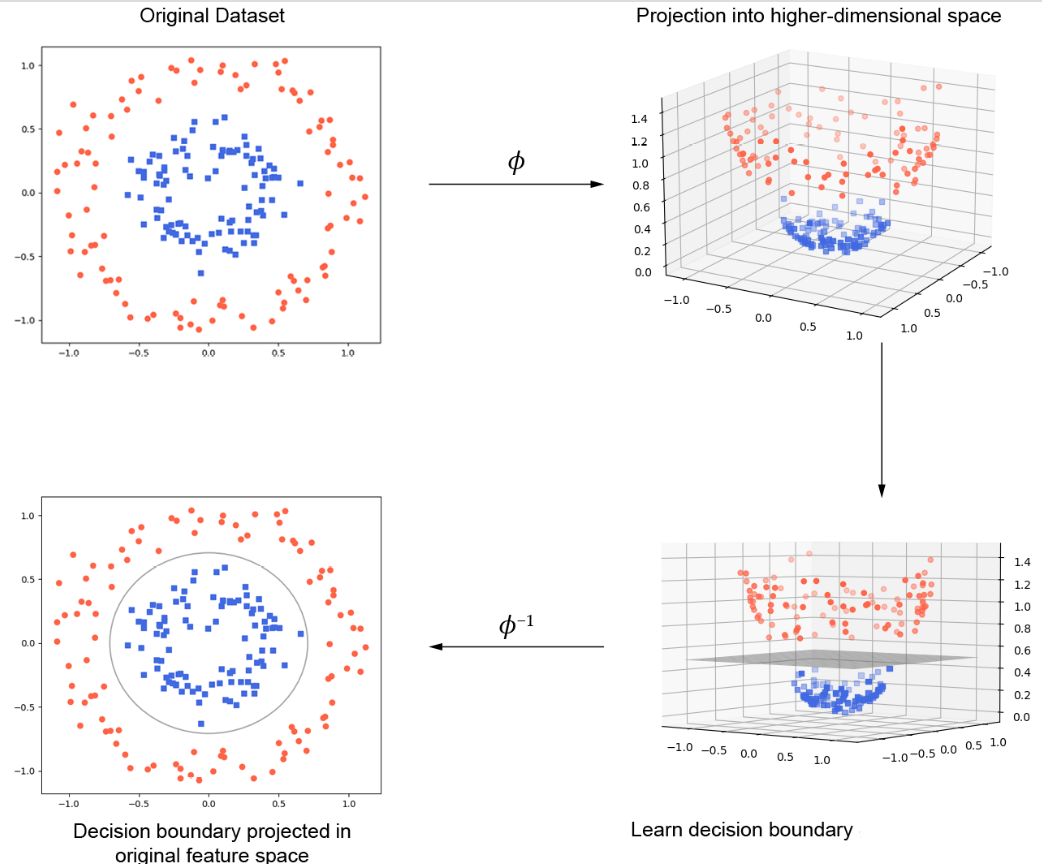
A kernel function is a function that takes two input vectors and returns a scalar value. The kernel function is used to map the input vectors into a higher-dimensional space where the classes are linearly separable. The most common kernel functions are the linear kernel, the polynomial kernel, and the radial basis function (RBF) kernel.
Let's try a support vector machine classifier for our data¶
First, we will use a linear kernel to classify the data. Same as before, we will use the SVC class from the sklearn.svm module. We will use the fit method to train the model on the training data and the predict method to make predictions on the test data.
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
## Define the classifier using make_pipeline
classifier = make_pipeline(StandardScaler(), SVC(kernel="linear"))
## Train the model
classifier.fit(X_train, y_train)
# Predict the test set
y_pred = classifier.predict(X_test)
# Calculate the accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
# Confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=le.classes_)
disp.plot(cmap=plt.cm.Blues, values_format='d', colorbar=False);
Accuracy: 0.90
Let's try to classify the data using a non-linear kernel. We will use the radial basis function (RBF) kernel, which is the default kernel for the SVC class. The RBF kernel is defined as:
$$K(x, x') = \exp(-\gamma ||x - x'||^2)$$
where $\gamma$ is a hyperparameter that controls the smoothness of the decision boundary.
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
## Define the classifier using make_pipeline and the RBF kernel
gamma = 0.03 ## gamma is a hyperparameter of the RBF kernel
classifier = make_pipeline(StandardScaler(), SVC(kernel="rbf", gamma=gamma))
## Train the model
classifier.fit(X_train, y_train)
## Predict the test set
y_pred = classifier.predict(X_test)
## Calculate the accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
## Confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=le.classes_)
disp.plot(cmap=plt.cm.Blues, values_format='d', colorbar=False);
Accuracy: 0.94
The gamma parameter of the RBF kernel controls the smoothness of the decision boundary.
- A larger value of gamma will result in a more complex decision boundary, which can lead to overfitting.
- A smaller value of gamma will result in a smoother decision boundary, which can lead to underfitting.
How can we choose the best value of gamma? Let's try a few different values and see how they affect the accuracy of the classifier on the training and test data.
Question to consider:
- How will the training accuracy change as we increase the value of gamma?
- How will the test accuracy change as we increase the value of gamma?
# Function to train SVM and return accuracies
def train_svm_and_get_accuracies(gamma, X_train, y_train, X_test, y_test):
classifier = make_pipeline(StandardScaler(), SVC(kernel="rbf", gamma=gamma))
classifier.fit(X_train, y_train)
# Calculate accuracies
train_accuracy = accuracy_score(y_train, classifier.predict(X_train))
test_accuracy = accuracy_score(y_test, classifier.predict(X_test))
return train_accuracy, test_accuracy
# Generate a range of gamma values
gamma_values = np.logspace(-4, 1, 20)
# Lists to store accuracies
train_accuracies = []
test_accuracies = []
# Calculate accuracies for each gamma value
for gamma in gamma_values:
train_acc, test_acc = train_svm_and_get_accuracies(gamma, X_train, y_train, X_test, y_test)
train_accuracies.append(train_acc)
test_accuracies.append(test_acc)
# Plot accuracy vs gamma
plt.figure(figsize=(12, 8))
plt.semilogx(gamma_values, train_accuracies, label='Training Accuracy', marker='o')
plt.semilogx(gamma_values, test_accuracies, label='Test Accuracy', marker='s')
plt.xlabel('Gamma')
plt.ylabel('Accuracy')
plt.title('Accuracy vs Gamma (SVM with RBF Kernel)')
plt.legend()
plt.grid(True)
idx = np.argmax(test_accuracies)
best_gamma = gamma_values[idx]
plt.axvline(x=best_gamma, color='r', linestyle='--', label=f'Best Gamma: {best_gamma:.2f}\nTraining Accuracy: {train_accuracies[idx]:.2f}\nTest Accuracy: {test_accuracies[idx]:.2f}')
plt.text(10**((-3 + np.log10(best_gamma)) / 2), 0.7, 'High Bias\nUnderfitting', ha='center')
plt.text(10**((1 + np.log10(best_gamma)) / 2), 0.7, 'High Variance\nOverfitting', ha='center')
plt.legend()
plt.show()
Decision tree¶
Let's try a Decision Trees approach which is another supervised machine learning algorithm for classification
Decision Trees are a type of flowchart-like structure where internal nodes represent decisions based on the input features, branches represent the outcome of these decisions, and leaf nodes represent the final output or class label. The primary goal of a decision tree is to recursively split the data into subsets based on feature values that maximize the separation between the classes.
Why use Decision Trees?
- Easy to understand and interpret: Decision Trees are human-readable and can be visualized, making them easy to understand and interpret even for those with limited machine learning experience.
- Minimal data preprocessing: Decision Trees do not require extensive data preprocessing, such as scaling or normalization, as they can handle both numerical and categorical features.
- Non-linear relationships: Decision Trees can model complex, non-linear relationships between features and target variables.
- Feature importance: Decision Trees can provide insights into feature importance, helping to identify the most relevant features for the problem at hand.
Implement the DecisionTreeClassifier¶
from sklearn.tree import DecisionTreeClassifier
## Define the decision tree classifier
classifier = DecisionTreeClassifier()
## Train the model
classifier.fit(X_train, y_train)
## Make predictions on the test set
y_pred = classifier.predict(X_test)
## Evaluate the classifier
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
Accuracy: 0.86
Plot the decision tree¶
from sklearn.tree import plot_tree
fig, ax = plt.subplots(figsize=(30, 20))
## Get the original class names
class_names = le.inverse_transform(np.unique(y)).astype(str)
## Visualize the decision tree
plot_tree(classifier, filled=True, feature_names=columns, class_names=class_names, ax=ax);
What aspects of the data are important for the classification?¶
We want to be able to readily determine what data fields are the most important for the decision tree. We can do that by determining "feature importance." The code below extracts and displays the importance score, also known as Gini importance or Mean Decrease Impurity, which is a measure of how much a feature contributes to the decision-making process of the decision tree model.
## Get the feature importances from the classifier
importances = classifier.feature_importances_
## Pair the feature names with their corresponding importances
feature_importances = list(zip(columns, importances))
## Create a DataFrame from the feature importances
df_feature_importances = pd.DataFrame(feature_importances, columns=['Feature', 'Importance'])
## Sort the feature importances in descending order
df_feature_importances = df_feature_importances.sort_values(by='Importance', ascending=False)
## Reset the index and drop the old index column
df_feature_importances.reset_index(drop=True, inplace=True)
## Display the sorted feature importances
display(df_feature_importances)
| Feature | Importance | |
|---|---|---|
| 0 | Sr_ppm | 0.287424 |
| 1 | TiO2_wt_percent | 0.269707 |
| 2 | Y_ppm | 0.128004 |
| 3 | Ni_ppm | 0.060744 |
| 4 | K2O_wt_percent | 0.048790 |
| 5 | MgO_wt_percent | 0.036844 |
| 6 | Sm_ppm | 0.036048 |
| 7 | SiO2_wt_percent | 0.031882 |
| 8 | Ce_ppm | 0.010861 |
| 9 | Zr_ppm | 0.008846 |
| 10 | Eu_ppm | 0.008293 |
| 11 | 87Sr/86Sr | 0.008082 |
| 12 | Al2O3_wt_percent | 0.007582 |
| 13 | MnO_wt_percent | 0.005618 |
| 14 | Cr_ppm | 0.005308 |
| 15 | Ba_ppm | 0.005213 |
| 16 | Zn_ppm | 0.005178 |
| 17 | Tb_ppm | 0.005119 |
| 18 | Hf_ppm | 0.005061 |
| 19 | Lu_ppm | 0.003895 |
| 20 | P2O5(wt%) | 0.003791 |
| 21 | V_ppm | 0.003791 |
| 22 | Cs_ppm | 0.003323 |
| 23 | Co_ppm | 0.002843 |
| 24 | U_ppm | 0.002810 |
| 25 | Fe2O3_wt_percent | 0.002704 |
| 26 | 206Pb/204Pb | 0.002238 |
| 27 | Gd_ppm | 0.000000 |
| 28 | La_ppm | 0.000000 |
| 29 | Pr_ppm | 0.000000 |
| 30 | Nd_ppm | 0.000000 |
| 31 | CaO_wt_percent | 0.000000 |
| 32 | FeO_wt_percent | 0.000000 |
| 33 | Na2O_wt_percent | 0.000000 |
| 34 | Dy_ppm | 0.000000 |
| 35 | Rb_ppm | 0.000000 |
| 36 | Ga_ppm | 0.000000 |
| 37 | Cu_ppm | 0.000000 |
| 38 | Ho_ppm | 0.000000 |
| 39 | Tm_ppm | 0.000000 |
| 40 | Er_ppm | 0.000000 |
| 41 | Yb_ppm | 0.000000 |
| 42 | Sc_ppm | 0.000000 |
| 43 | Ta_ppm | 0.000000 |
| 44 | Sn_ppm | 0.000000 |
| 45 | Nb_ppm | 0.000000 |
| 46 | Pb_ppm | 0.000000 |
| 47 | 143Nd/144Nd | 0.000000 |
| 48 | Th_ppm | 0.000000 |
| 49 | 207Pb/204Pb | 0.000000 |
| 50 | 208Pb/204Pb | 0.000000 |
Question
If we were going to build a classifier on just two variables, which should be pick?
Exploring other classification algorithms¶
If you go to the scikit-learn homepage you will find many available classifiers: https://scikit-learn.org/stable/index.html. They are nicely illustrated in this code from the scikit-learn documentation.
# Code source: Gaël Varoquaux
# Andreas Müller
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons, make_circles, make_classification
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
h = .02 # step size in the mesh
names = ["Nearest Neighbors", "Linear SVM", "RBF SVM", "Gaussian Process",
"Decision Tree", "Random Forest", "Neural Net", "AdaBoost",
"Naive Bayes", "QDA"]
classifiers = [
KNeighborsClassifier(3),
SVC(kernel="linear", C=0.025),
SVC(gamma=2, C=1),
GaussianProcessClassifier(1.0 * RBF(1.0)),
DecisionTreeClassifier(max_depth=5),
RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1),
MLPClassifier(alpha=1, max_iter=1000),
AdaBoostClassifier(),
GaussianNB(),
QuadraticDiscriminantAnalysis()]
X, y = make_classification(n_features=2, n_redundant=0, n_informative=2,
random_state=1, n_clusters_per_class=1)
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_separable = (X, y)
datasets = [make_moons(noise=0.3, random_state=0),
make_circles(noise=0.2, factor=0.5, random_state=1),
linearly_separable
]
figure = plt.figure(figsize=(27, 9))
i = 1
# iterate over datasets
for ds_cnt, ds in enumerate(datasets):
# preprocess dataset, split into training and test part
X, y = ds
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=.4, random_state=41)
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# just plot the dataset first
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
if ds_cnt == 0:
ax.set_title("Input data")
# Plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
# Plot the testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6,
edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
i += 1
# iterate over classifiers
for name, clf in zip(names, classifiers):
ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
if hasattr(clf, "decision_function"):
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
else:
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
# Put the result into a color plot
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)
# Plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
# Plot the testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright,
edgecolors='k', alpha=0.6)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
if ds_cnt == 0:
ax.set_title(name)
ax.text(xx.max() - .3, yy.min() + .3, ('%.2f' % score).lstrip('0'),
size=15, horizontalalignment='right')
i += 1
plt.tight_layout()
plt.show()
/home/vscode/.local/lib/python3.10/site-packages/sklearn/ensemble/_weight_boosting.py:527: FutureWarning: The SAMME.R algorithm (the default) is deprecated and will be removed in 1.6. Use the SAMME algorithm to circumvent this warning. warnings.warn( /home/vscode/.local/lib/python3.10/site-packages/sklearn/ensemble/_weight_boosting.py:527: FutureWarning: The SAMME.R algorithm (the default) is deprecated and will be removed in 1.6. Use the SAMME algorithm to circumvent this warning. warnings.warn( /home/vscode/.local/lib/python3.10/site-packages/sklearn/ensemble/_weight_boosting.py:527: FutureWarning: The SAMME.R algorithm (the default) is deprecated and will be removed in 1.6. Use the SAMME algorithm to circumvent this warning. warnings.warn(
Normalize the data¶
The decision tree suggested that Ti and Sr were the biggest differentiators. Let's have a look at Ti (wt %) vs Sr (ppm) and apply different classifying algorithms. For many of these algorithms, it is essential to normalize the data. For example, the nearest neighbor is a distance. Consider that in the TiO2 (wt%) vs. Sr (ppm) or V (ppm) the y-axis and x-axis are so different (in part because of different units). So we need to normalize the data.
We can use the sklearn.preprocessing function StandardScaler to help us here.
Let's make a basalt_data_Ti_Sr dataframe and then apply the StandardScaler approach.
basalt_data_Ti_Sr = basalt_data[(~basalt_data['TiO2_wt_percent'].isna()) & (~basalt_data['Sr_ppm'].isna())]
from sklearn.preprocessing import StandardScaler
# Extract the necessary features and target variable
X = basalt_data_Ti_Sr[['TiO2_wt_percent', 'Sr_ppm']].values
y = basalt_data_Ti_Sr['affinity'].values
# Encode the target variable 'affinity' using LabelEncoder
le = LabelEncoder()
y = le.fit_transform(y)
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=41)
# Instantiate the scaler
scaler = StandardScaler()
# Fit the scaler to the training data and transform it
X_train_normalized = scaler.fit_transform(X_train)
# Transform the testing data using the fitted scaler
X_test_normalized = scaler.transform(X_test)
K-nearest neighbors¶
Let's try another classification method called K-nearest neighbors (KNN) which is a simple and intuitive algorithm for classification. The basic idea behind KNN is to classify a new data point based on the majority class of its K nearest neighbors in the feature space.
Apply the KNeighborsClassifier to the two most important features from the decision tree classifier.
from sklearn.neighbors import KNeighborsClassifier
## Extract the necessary features and target variable; Filter out rows with nan values
basalt_data = basalt_data[(~basalt_data['TiO2_wt_percent'].isna()) & (~basalt_data['Sr_ppm'].isna())]
## Prepare the data into features (X) and target (y); Encode the target variable
X = basalt_data[['TiO2_wt_percent', 'Sr_ppm']].values
y = le.fit_transform(basalt_data['affinity'])
## Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=41)
## Define the KNN classifier with 3 neighbors using make_pipeline
classifier = make_pipeline(StandardScaler(), KNeighborsClassifier(3))
## Train the model
classifier.fit(X_train, y_train)
## Make predictions on the test set
y_pred = classifier.predict(X_test)
## Evaluate the classifier
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
Accuracy: 0.94
Let's plot the decision boundary for the KNN classifier. The decision boundary is the line that separates the different classes in the feature space.
# Create a meshgrid
x_min, x_max = X_test[:, 0].min() - 1, X_test[:, 0].max() + 1
y_min, y_max = X_test[:, 1].min() - 1, X_test[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 20), np.linspace(y_min, y_max, 20))
# Classify the grid points using the classifier
grid = np.c_[xx.ravel(), yy.ravel()]
grid_classes = classifier.predict(grid)
# Reshape the predicted class labels to match the shape of the input grid
grid_classes = grid_classes.reshape(xx.shape)
# Plot the decision boundary and the test data points
cmap = ListedColormap(['C2', 'C0', 'C1'])
plt.figure()
plt.contourf(xx, yy, grid_classes, cmap=cmap, alpha=0.6)
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cmap, edgecolors='k', marker='o', s=50)
# Add a legend
cbar = plt.colorbar(ticks=[0.375, 1., 1.625])
cbar.set_ticklabels(le.inverse_transform([0, 1, 2]))
plt.xlabel('Normalized TiO2_wt_percent')
plt.ylabel('Normalized Sr_ppm')
plt.title('Classifier (Test Data with Decision Boundary)')
plt.show()
A word of warning¶
As a word of warning, we shouldn't get too carried away. Clearly, there are complexities related to this approach (our accuracy scores aren't that high). There are other types of contextual data that can give insight. For example, Shervais (1982) notes that:
"More specific evaluation of the tectonic setting of these and other ophiolites requires application of detailed geologic and petrologic data as well as geochemistry. The Ti/V discrimination diagram, however, is a potentially powerful adjunct to these techniques."
Vermeesch adds to this point by writing:
"no classification method based solely on geochemical data will ever be able to perfectly determine the tectonic affinity of basaltic rocks (or other rocks for that matter) simply because there is a lot of actual overlap between the geochemistry of the different tectonic settings. Notably IABs have a much wider range of compositions than either MORBs or OIBs. Therefore, geochemical classification should never be the only basis for determining tectonic affinity. This is especially the case for rocks that have undergone alteration. In such cases, mobile elements such as Sr, which have great discriminative power, cannot be used."
Additionally, we would like to be able to assign physical processes to any classification given that we are seeking insight into how the Earth works.