Neural Networks with PyTorch¶

Run in Google Colab

Note: If you are running this in a colab notebook, we recommend you enable a free GPU by going:

Runtime   →   Change runtime type   →   Hardware Accelerator: GPU

GPUs are commonly used to accelerate training of deep learning models. If you want to learn more about GPUs or even TPUs for training nerual networks, check out this short video.

This notebooks shows how to define and train a simple modern Neural Network with PyTorch.

We will use the MNIST dataset, which is a dataset of 60,000 28x28 grayscale images of the 10 digits, along with a test set of 10,000 images.

The dateaset is very popular and is often used as a "Hello World" example in the field of Machine Learning. It is a good dataset to start with, as it is small and easy to work with.

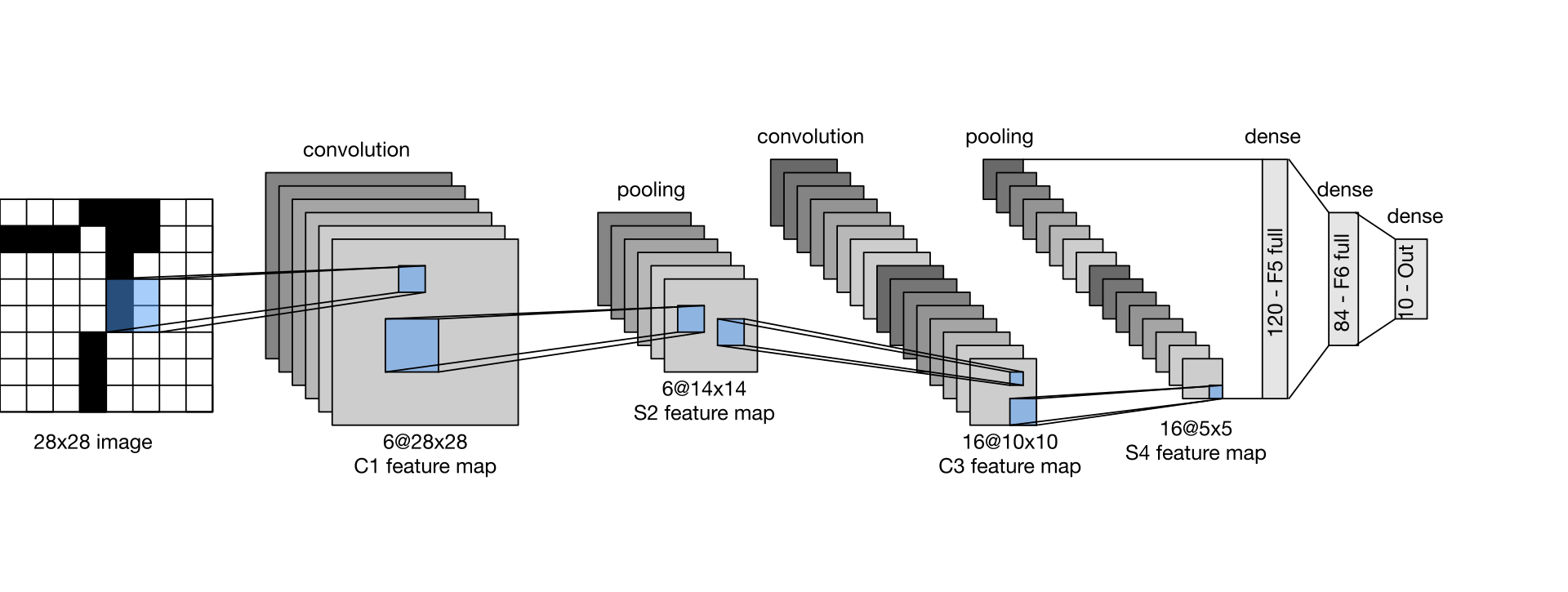
For this small dataset, we will use the socalled "LeNet" architecture is used here. It is a simple convolutional neural network, which was introduced by Yann LeCun in 1998. It is a simple and effective architecture for small image datasets. You can read more about the model on Wikipedia.

In [1]:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay
import torch
from torch import nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
from tqdm import tqdm

import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import fetch_openml from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay import torch from torch import nn import torch.nn.functional as F import torch.optim as optim from torch.utils.data import DataLoader, TensorDataset from tqdm import tqdm

In [2]:

## Set random seed
torch.manual_seed(0)
torch.cuda.manual_seed(0)
np.random.seed(0)

## Set random seed torch.manual_seed(0) torch.cuda.manual_seed(0) np.random.seed(0)

Loading Data¶

Using SciKit-Learns fetch_openml to load MNIST data.

Each image of the MNIST dataset is encoded in a 784 dimensional vector, representing a 28 x 28 pixel image.

Each pixel has a value between 0 and 255, corresponding to the grey-value of a pixel.

In [3]:

mnist = fetch_openml('mnist_784', as_frame=False)

mnist = fetch_openml('mnist_784', as_frame=False)

In [4]:

print(f"MNIST data shape: {mnist.data.shape}, data type: {mnist.data.dtype}")
print(f"MNIST target shape: {mnist.target.shape}, target type: {mnist.target.dtype}")

print(f"MNIST data shape: {mnist.data.shape}, data type: {mnist.data.dtype}") print(f"MNIST target shape: {mnist.target.shape}, target type: {mnist.target.dtype}")

MNIST data shape: (70000, 784), data type: int64
MNIST target shape: (70000,), target type: object

Preprocessing Data¶

The above featch_mldata method to load MNIST returns data and target as uint8 which we convert to float32 and int64 respectively.

To avoid big weights that deal with the pixel values from between [0, 255], we scale X down. A commonly used range is [0, 1].

In [5]:

## Make sure the data is float32 and the labels are int64
X = mnist.data.astype('float32')
y = mnist.target.astype('int64')

## Normalize the data to [0, 1]. Hint: the raw pixel values are in [0, 255].
X /= 255.0
print(f"{X.min() = }, {X.max() = }")

## Make sure the data is float32 and the labels are int64 X = mnist.data.astype('float32') y = mnist.target.astype('int64') ## Normalize the data to [0, 1]. Hint: the raw pixel values are in [0, 255]. X /= 255.0 print(f"{X.min() = }, {X.max() = }")

X.min() = 0.0, X.max() = 1.0

Same as prevoious lectures, let split the data into training and testing sets.

In [6]:

## Split data into training and testing sets using 30% of the data for testing and random seed 42
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

## Split data into training and testing sets using 30% of the data for testing and random seed 42 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

Visualize a selection of training images and their labels¶

In [7]:

## Define a function to plot a selection of images and their labels
def plot_example(X, y, n_samples=10):
    """Plot the first n_samples images and their labels in a row."""
    fig, axes = plt.subplots(1, n_samples, figsize=(2*n_samples, 4))
    for i, ax in enumerate(axes):
        ax.imshow(X[i].reshape(28, 28), cmap='gray')
        ax.set_title(y[i], fontsize=32)
        ax.axis('off')
    plt.tight_layout()
    plt.show()

## Define a function to plot a selection of images and their labels def plot_example(X, y, n_samples=10): """Plot the first n_samples images and their labels in a row.""" fig, axes = plt.subplots(1, n_samples, figsize=(2*n_samples, 4)) for i, ax in enumerate(axes): ax.imshow(X[i].reshape(28, 28), cmap='gray') ax.set_title(y[i], fontsize=32) ax.axis('off') plt.tight_layout() plt.show()

In [8]:

## Plot the first 10 images from the training set
plot_example(X_train, y_train, n_samples=10)

## Plot the first 10 images from the training set plot_example(X_train, y_train, n_samples=10)

Build Neural Network with PyTorch¶

In the previous lecture, we have built a simple fully connected neural network with one hidden layer for both linear regression and classification tasks. Let's first try a similar network for the classification task of MNIST.

Note the dataset is much larger than our previous examples, so we need to adjust the network size accordingly. (It is still tiny compared to modern standards)

Let's think about the network architecture:

• Input layer: 784 dimensions (28x28). This is defined by the MNIST data shape.
• Hidden layer: 98 (= 784 / 8). This is a free parameter that we can choose.
• Output layer: 10 neurons, representing digits 0 - 9. This is defined by the number of classes in the dataset.

• Prepare the data for training and testing

In [9]:

## Convert data to PyTorch tensors
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.int64)
X_test_tensor = torch.tensor(X_test, dtype=torch.float32)
y_test_tensor = torch.tensor(y_test, dtype=torch.int64)

## Convert data to PyTorch tensors X_train_tensor = torch.tensor(X_train, dtype=torch.float32) y_train_tensor = torch.tensor(y_train, dtype=torch.int64) X_test_tensor = torch.tensor(X_test, dtype=torch.float32) y_test_tensor = torch.tensor(y_test, dtype=torch.int64)

• Build a simple fully connected neural network in PyTorch's framework.

In [10]:

## Define the network architecture: A simple fully connected neural network
class FCN(nn.Module):
    def __init__(
            self,
            input_dim=28*28,
            hidden_dim=28*4,
            output_dim=10,
            dropout=0.5,
    ):
        super(FCN, self).__init__()
        ## Define the neural network layers
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, **kwargs):
        ## Apply the neural network layers
        x = self.fc1(x)
        x = F.relu(x)
        x = self.dropout(x)
        x = self.fc2(x)
        return x

## Define the network architecture: A simple fully connected neural network class FCN(nn.Module): def __init__( self, input_dim=28*28, hidden_dim=28*4, output_dim=10, dropout=0.5, ): super(FCN, self).__init__() ## Define the neural network layers self.fc1 = nn.Linear(input_dim, hidden_dim) self.fc2 = nn.Linear(hidden_dim, output_dim) self.dropout = nn.Dropout(dropout) def forward(self, x, **kwargs): ## Apply the neural network layers x = self.fc1(x) x = F.relu(x) x = self.dropout(x) x = self.fc2(x) return x

In [11]:

## Define the model dimensions
mnist_dim = X.shape[1]
hidden_dim = int(mnist_dim/8)
output_dim = len(np.unique(mnist.target))

## Define the model, loss function, and optimizer
model = FCN(input_dim=mnist_dim, hidden_dim=hidden_dim, output_dim=output_dim)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

## Define the device to choose the fastest for training
## MPS for Apple Silicon, CUDA for NVidia GPUs, and CPU otherwise
device = 'mps' if torch.backends.mps.is_available() else 'cuda' if torch.cuda.is_available() else 'cpu'

## Define fit function
def fit(model, X_train, y_train, epochs=100):
    dataloader = DataLoader(dataset=TensorDataset(X_train, y_train), batch_size=128, shuffle=True, drop_last=True)
    model.to(device)

    ## set the model to training mode
    model.train()
    losses = []
    for epoch in range(epochs):
        loss = 0
        for X_train, y_train in tqdm(dataloader, desc=f'Training Epoch {epoch+1}/{epochs}'):
            X_train = X_train.to(device)
            y_train = y_train.to(device)
            ## zero the gradients
            optimizer.zero_grad()

            ## get the model predictions
            outputs = model(X_train)
            ## calculate the loss
            batch_loss = criterion(outputs, y_train)
            batch_loss.backward()
            ## update the weights
            optimizer.step()
            
            loss += batch_loss.item()

        # average loss per batch
        loss = loss / len(dataloader)
        losses.append(loss)

        print(f'Epoch {epoch+1}/{epochs}: Loss: {loss:.4f}')

    return losses

## Define predict function
def predict(model, X):
    dataloader = DataLoader(dataset=TensorDataset(X), batch_size=128, drop_last=False)
    ## set the model to evaluation mode
    model.eval()
    device = next(model.parameters()).device
    with torch.no_grad():
        predicted = []
        for X, in tqdm(dataloader, desc='Predicting'):
            X = X.to(device)
            
            ## get the model predictions
            outputs = model(X)

            _, predicted_batch = torch.max(outputs, 1)
            predicted.append(predicted_batch.cpu())
    return torch.cat(predicted)

## Train the model
losses = fit(model, X_train_tensor, y_train_tensor, epochs=15)

## Plot the loss
plt.figure()
plt.plot(losses)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()

## Define the model dimensions mnist_dim = X.shape[1] hidden_dim = int(mnist_dim/8) output_dim = len(np.unique(mnist.target)) ## Define the model, loss function, and optimizer model = FCN(input_dim=mnist_dim, hidden_dim=hidden_dim, output_dim=output_dim) criterion = nn.CrossEntropyLoss() optimizer = optim.Adam(model.parameters(), lr=0.001) ## Define the device to choose the fastest for training ## MPS for Apple Silicon, CUDA for NVidia GPUs, and CPU otherwise device = 'mps' if torch.backends.mps.is_available() else 'cuda' if torch.cuda.is_available() else 'cpu' ## Define fit function def fit(model, X_train, y_train, epochs=100): dataloader = DataLoader(dataset=TensorDataset(X_train, y_train), batch_size=128, shuffle=True, drop_last=True) model.to(device) ## set the model to training mode model.train() losses = [] for epoch in range(epochs): loss = 0 for X_train, y_train in tqdm(dataloader, desc=f'Training Epoch {epoch+1}/{epochs}'): X_train = X_train.to(device) y_train = y_train.to(device) ## zero the gradients optimizer.zero_grad() ## get the model predictions outputs = model(X_train) ## calculate the loss batch_loss = criterion(outputs, y_train) batch_loss.backward() ## update the weights optimizer.step() loss += batch_loss.item() # average loss per batch loss = loss / len(dataloader) losses.append(loss) print(f'Epoch {epoch+1}/{epochs}: Loss: {loss:.4f}') return losses ## Define predict function def predict(model, X): dataloader = DataLoader(dataset=TensorDataset(X), batch_size=128, drop_last=False) ## set the model to evaluation mode model.eval() device = next(model.parameters()).device with torch.no_grad(): predicted = [] for X, in tqdm(dataloader, desc='Predicting'): X = X.to(device) ## get the model predictions outputs = model(X) _, predicted_batch = torch.max(outputs, 1) predicted.append(predicted_batch.cpu()) return torch.cat(predicted) ## Train the model losses = fit(model, X_train_tensor, y_train_tensor, epochs=15) ## Plot the loss plt.figure() plt.plot(losses) plt.xlabel('Epochs') plt.ylabel('Loss') plt.show()

Training Epoch 1/15: 100%|██████████| 382/382 [00:04<00:00, 84.52it/s] 

Epoch 1/15: Loss: 0.6224

Training Epoch 2/15: 100%|██████████| 382/382 [00:03<00:00, 97.92it/s] 

Epoch 2/15: Loss: 0.3276

Training Epoch 3/15: 100%|██████████| 382/382 [00:03<00:00, 104.05it/s]

Epoch 3/15: Loss: 0.2684

Training Epoch 4/15: 100%|██████████| 382/382 [00:04<00:00, 93.66it/s] 

Epoch 4/15: Loss: 0.2408

Training Epoch 5/15: 100%|██████████| 382/382 [00:03<00:00, 99.05it/s] 

Epoch 5/15: Loss: 0.2120

Training Epoch 6/15: 100%|██████████| 382/382 [00:03<00:00, 102.76it/s]

Epoch 6/15: Loss: 0.1991

Training Epoch 7/15: 100%|██████████| 382/382 [00:03<00:00, 100.87it/s]

Epoch 7/15: Loss: 0.1863

Training Epoch 8/15: 100%|██████████| 382/382 [00:03<00:00, 103.79it/s]

Epoch 8/15: Loss: 0.1715

Training Epoch 9/15: 100%|██████████| 382/382 [00:04<00:00, 82.94it/s] 

Epoch 9/15: Loss: 0.1644

Training Epoch 10/15: 100%|██████████| 382/382 [00:03<00:00, 126.21it/s]

Epoch 10/15: Loss: 0.1596

Training Epoch 11/15: 100%|██████████| 382/382 [00:04<00:00, 77.86it/s] 

Epoch 11/15: Loss: 0.1561

Training Epoch 12/15: 100%|██████████| 382/382 [00:04<00:00, 82.26it/s] 

Epoch 12/15: Loss: 0.1450

Training Epoch 13/15: 100%|██████████| 382/382 [00:03<00:00, 97.77it/s] 

Epoch 13/15: Loss: 0.1407

Training Epoch 14/15: 100%|██████████| 382/382 [00:04<00:00, 89.12it/s] 

Epoch 14/15: Loss: 0.1392

Training Epoch 15/15: 100%|██████████| 382/382 [00:03<00:00, 97.44it/s] 

Epoch 15/15: Loss: 0.1344

• Evaluate the model on the test set. This is same as the previous lecture.

In [12]:

## Predict on the test set
y_pred_tensor = predict(model, X_test_tensor)
y_pred = y_pred_tensor.numpy()

## Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.4f}')

## Confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=np.arange(len(np.unique(y))))
disp.plot(cmap=plt.cm.Blues, values_format='d', colorbar=False);

## Predict on the test set y_pred_tensor = predict(model, X_test_tensor) y_pred = y_pred_tensor.numpy() ## Calculate accuracy accuracy = accuracy_score(y_test, y_pred) print(f'Accuracy: {accuracy:.4f}') ## Confusion matrix conf_matrix = confusion_matrix(y_test, y_pred) disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=np.arange(len(np.unique(y)))) disp.plot(cmap=plt.cm.Blues, values_format='d', colorbar=False);

Predicting: 100%|██████████| 165/165 [00:00<00:00, 224.32it/s]

Accuracy: 0.9686

What accuracy did you get? Is it above 95%?

An accuracy of above 95% for a network with only one hidden layer is not too bad.

Let's take a look at some predictions that went wrong:

In [13]:

error_mask_fcn = y_pred != y_test
plot_example(X_test[error_mask_fcn], y_pred[error_mask_fcn], n_samples=10)

error_mask_fcn = y_pred != y_test plot_example(X_test[error_mask_fcn], y_pred[error_mask_fcn], n_samples=10)

Are these errors reasonable?

Convolutional Network¶

To further improve the performance, let's try a convolutional neural network (CNN) for MNIST.

The 2D convolutional layer expects a 4 dimensional tensor as input. The dimensions represent:

• Batch size
• Number of channel
• Height
• Width

So we need to reshape the MNIST data to have the right shape. MNIST data has only one channel. As stated above, each MNIST vector represents a 28x28 pixel image. Hence, the resulting shape for PyTorch tensor needs to be (x, 1, 28, 28).

• Prepare the data for training and testing

In [14]:

## Convert data to PyTorch tensors and reshape to 4D tensor (batch_size, channel, height, width)
X_train_tensor = torch.tensor(X_train, dtype=torch.float32).reshape(-1, 1, 28, 28)
X_test_tensor = torch.tensor(X_test, dtype=torch.float32).reshape(-1, 1, 28, 28)
y_train_tensor = torch.tensor(y_train, dtype=torch.int64)
y_test_tensor = torch.tensor(y_test, dtype=torch.int64)

## Convert data to PyTorch tensors and reshape to 4D tensor (batch_size, channel, height, width) X_train_tensor = torch.tensor(X_train, dtype=torch.float32).reshape(-1, 1, 28, 28) X_test_tensor = torch.tensor(X_test, dtype=torch.float32).reshape(-1, 1, 28, 28) y_train_tensor = torch.tensor(y_train, dtype=torch.int64) y_test_tensor = torch.tensor(y_test, dtype=torch.int64)

• Build a simple convolutional neural network in PyTorch's framework.

In [15]:

## Define the network architecture: A simple convolutional neural network
class CNN(nn.Module):
    def __init__(self, input_dim=28*28, hidden_dim=112, output_dim=10, dropout=0.5):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, kernel_size=3)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3)
        self.conv1_drop = nn.Dropout2d(p=dropout)
        self.conv2_drop = nn.Dropout2d(p=dropout)
        num_features = 64 * int((input_dim**0.5 // 4 - 2)**2)
        self.fc1 = nn.Linear(num_features, hidden_dim) # 1600 = number channels * width * height
        self.fc2 = nn.Linear(hidden_dim, output_dim)
        self.fc1_drop = nn.Dropout(p=dropout)

    def forward(self, x):
    
        x = self.conv1(x)
        x = F.relu(x)
        x = F.max_pool2d(x, 2)
        x = self.conv1_drop(x)

        x = self.conv2(x)
        x = F.relu(x)
        x = F.max_pool2d(x, 2)
        x = self.conv2_drop(x)
        
        # flatten over channel, height and width        
        x = x.view(x.size(0), -1)
        
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc1_drop(x)
        x = self.fc2(x)

        return x

## Define the network architecture: A simple convolutional neural network class CNN(nn.Module): def __init__(self, input_dim=28*28, hidden_dim=112, output_dim=10, dropout=0.5): super(CNN, self).__init__() self.conv1 = nn.Conv2d(1, 32, kernel_size=3) self.conv2 = nn.Conv2d(32, 64, kernel_size=3) self.conv1_drop = nn.Dropout2d(p=dropout) self.conv2_drop = nn.Dropout2d(p=dropout) num_features = 64 * int((input_dim**0.5 // 4 - 2)**2) self.fc1 = nn.Linear(num_features, hidden_dim) # 1600 = number channels * width * height self.fc2 = nn.Linear(hidden_dim, output_dim) self.fc1_drop = nn.Dropout(p=dropout) def forward(self, x): x = self.conv1(x) x = F.relu(x) x = F.max_pool2d(x, 2) x = self.conv1_drop(x) x = self.conv2(x) x = F.relu(x) x = F.max_pool2d(x, 2) x = self.conv2_drop(x) # flatten over channel, height and width x = x.view(x.size(0), -1) x = self.fc1(x) x = F.relu(x) x = self.fc1_drop(x) x = self.fc2(x) return x

In [16]:

## Initialize the network parameters, loss function, optimizer, and device
mnist_dim = X.shape[1]
hidden_dim = int(mnist_dim/8)
output_dim = len(np.unique(mnist.target))

## Define the model, loss function, and optimizer
model = CNN(input_dim=mnist_dim, hidden_dim=hidden_dim, output_dim=output_dim)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

## Define the device to choose the fastest for training
## MPS for Apple Silicon, CUDA for NVidia GPUs, and CPU otherwise
device = 'mps' if torch.backends.mps.is_available() else 'cuda' if torch.cuda.is_available() else 'cpu'

## Define fit function
def fit(model, X_train, y_train, epochs=100):

    dataloader = DataLoader(dataset=TensorDataset(X_train, y_train), batch_size=128, shuffle=True, drop_last=True)
    model.to(device)

    ## set the model to training mode
    model.train()
    losses = []
    for epoch in range(epochs):
        loss = 0
        for X_train, y_train in tqdm(dataloader, desc=f'Training Epoch {epoch+1}/{epochs}'):
            X_train = X_train.to(device)
            y_train = y_train.to(device)
            ## zero the gradients
            optimizer.zero_grad()

            ## get the model predictions
            outputs = model(X_train)
            ## calculate the loss
            batch_loss = criterion(outputs, y_train)
            ## update the weights
            batch_loss.backward()
            optimizer.step()

            loss += batch_loss.item()

        # average loss per batch
        loss = loss / len(dataloader)
        losses.append(loss)

        print(f'Epoch {epoch+1}/{epochs}: Loss: {loss:.4f}')

    return losses

## Define predict function
def predict(model, X):

    dataloader = DataLoader(dataset=TensorDataset(X), batch_size=128, drop_last=False)

    ## set the model to evaluation mode
    model.eval()
    device = next(model.parameters()).device
    with torch.no_grad():
        predicted = []
        for X, in tqdm(dataloader, desc='Predicting'):
            X = X.to(device)

            ## get the model predictions
            outputs = model(X)
            
            _, predicted_batch = torch.max(outputs, 1)
            predicted.append(predicted_batch.cpu())
    return torch.cat(predicted)

## Train the model
losses = fit(model, X_train_tensor, y_train_tensor, epochs=15)

## Plot the loss
plt.figure()
plt.plot(losses)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()

## Initialize the network parameters, loss function, optimizer, and device mnist_dim = X.shape[1] hidden_dim = int(mnist_dim/8) output_dim = len(np.unique(mnist.target)) ## Define the model, loss function, and optimizer model = CNN(input_dim=mnist_dim, hidden_dim=hidden_dim, output_dim=output_dim) criterion = nn.CrossEntropyLoss() optimizer = optim.Adam(model.parameters(), lr=0.001) ## Define the device to choose the fastest for training ## MPS for Apple Silicon, CUDA for NVidia GPUs, and CPU otherwise device = 'mps' if torch.backends.mps.is_available() else 'cuda' if torch.cuda.is_available() else 'cpu' ## Define fit function def fit(model, X_train, y_train, epochs=100): dataloader = DataLoader(dataset=TensorDataset(X_train, y_train), batch_size=128, shuffle=True, drop_last=True) model.to(device) ## set the model to training mode model.train() losses = [] for epoch in range(epochs): loss = 0 for X_train, y_train in tqdm(dataloader, desc=f'Training Epoch {epoch+1}/{epochs}'): X_train = X_train.to(device) y_train = y_train.to(device) ## zero the gradients optimizer.zero_grad() ## get the model predictions outputs = model(X_train) ## calculate the loss batch_loss = criterion(outputs, y_train) ## update the weights batch_loss.backward() optimizer.step() loss += batch_loss.item() # average loss per batch loss = loss / len(dataloader) losses.append(loss) print(f'Epoch {epoch+1}/{epochs}: Loss: {loss:.4f}') return losses ## Define predict function def predict(model, X): dataloader = DataLoader(dataset=TensorDataset(X), batch_size=128, drop_last=False) ## set the model to evaluation mode model.eval() device = next(model.parameters()).device with torch.no_grad(): predicted = [] for X, in tqdm(dataloader, desc='Predicting'): X = X.to(device) ## get the model predictions outputs = model(X) _, predicted_batch = torch.max(outputs, 1) predicted.append(predicted_batch.cpu()) return torch.cat(predicted) ## Train the model losses = fit(model, X_train_tensor, y_train_tensor, epochs=15) ## Plot the loss plt.figure() plt.plot(losses) plt.xlabel('Epochs') plt.ylabel('Loss') plt.show()

Training Epoch 1/15: 100%|██████████| 382/382 [00:08<00:00, 47.01it/s]

Epoch 1/15: Loss: 0.6035

Training Epoch 2/15: 100%|██████████| 382/382 [00:09<00:00, 38.57it/s]

Epoch 2/15: Loss: 0.2225

Training Epoch 3/15: 100%|██████████| 382/382 [00:07<00:00, 50.48it/s]

Epoch 3/15: Loss: 0.1759

Training Epoch 4/15: 100%|██████████| 382/382 [00:07<00:00, 54.05it/s]

Epoch 4/15: Loss: 0.1474

Training Epoch 5/15: 100%|██████████| 382/382 [00:08<00:00, 46.59it/s]

Epoch 5/15: Loss: 0.1295

Training Epoch 6/15: 100%|██████████| 382/382 [00:06<00:00, 57.71it/s]

Epoch 6/15: Loss: 0.1206

Training Epoch 7/15: 100%|██████████| 382/382 [00:05<00:00, 70.02it/s]

Epoch 7/15: Loss: 0.1133

Training Epoch 8/15: 100%|██████████| 382/382 [00:05<00:00, 71.75it/s]

Epoch 8/15: Loss: 0.1065

Training Epoch 9/15: 100%|██████████| 382/382 [00:04<00:00, 88.28it/s]

Epoch 9/15: Loss: 0.1030

Training Epoch 10/15: 100%|██████████| 382/382 [00:04<00:00, 86.71it/s]

Epoch 10/15: Loss: 0.0927

Training Epoch 11/15: 100%|██████████| 382/382 [00:04<00:00, 90.95it/s] 

Epoch 11/15: Loss: 0.0897

Training Epoch 12/15: 100%|██████████| 382/382 [00:05<00:00, 76.21it/s]

Epoch 12/15: Loss: 0.0867

Training Epoch 13/15: 100%|██████████| 382/382 [00:04<00:00, 82.52it/s]

Epoch 13/15: Loss: 0.0863

Training Epoch 14/15: 100%|██████████| 382/382 [00:05<00:00, 75.57it/s]

Epoch 14/15: Loss: 0.0816

Training Epoch 15/15: 100%|██████████| 382/382 [00:04<00:00, 91.97it/s] 

Epoch 15/15: Loss: 0.0769

In [17]:

## Predict on the test set
y_pred_tensor = predict(model, X_test_tensor)
y_pred = y_pred_tensor.numpy()

## Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.4f}')

## Confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=np.arange(len(np.unique(y))))
disp.plot(cmap=plt.cm.Blues, values_format='d', colorbar=False);

## Predict on the test set y_pred_tensor = predict(model, X_test_tensor) y_pred = y_pred_tensor.numpy() ## Calculate accuracy accuracy = accuracy_score(y_test, y_pred) print(f'Accuracy: {accuracy:.4f}') ## Confusion matrix conf_matrix = confusion_matrix(y_test, y_pred) disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=np.arange(len(np.unique(y)))) disp.plot(cmap=plt.cm.Blues, values_format='d', colorbar=False);

Predicting: 100%|██████████| 165/165 [00:00<00:00, 179.11it/s]

Accuracy: 0.9883

• What accuracy did you get? Is it better than the fully connected network?

An accuracy of >98% should suffice for this example!

Let's take a look at some predictions that went wrong:

In [18]:

error_mask_cnn = y_pred != y_test
plot_example(X_test[error_mask_cnn], y_pred[error_mask_cnn], n_samples=10)

error_mask_cnn = y_pred != y_test plot_example(X_test[error_mask_cnn], y_pred[error_mask_cnn], n_samples=10)

• Let's further look at the accuracy of the convolutional network model (CNN) on the misclassified examples previously by the fully connected network (FCN).

In [19]:

accuracy = accuracy_score(y_test[error_mask_fcn], y_pred[error_mask_fcn])
print(f"Accuracy: {accuracy:.4f}")

accuracy = accuracy_score(y_test[error_mask_fcn], y_pred[error_mask_fcn]) print(f"Accuracy: {accuracy:.4f}")

Accuracy: 0.7318

About 70% of the previously misclassified images are now correctly identified.

Let's take a look at some of the misclassified examples before:

In [20]:

plot_example(X_test[error_mask_fcn], y_pred[error_mask_fcn])

plot_example(X_test[error_mask_fcn], y_pred[error_mask_fcn])

• Last questions. Please take a look at the training loops of the fully connected network and the convolutional network. Comment on the similarities and differences.

You can see although the network architecture is different, the training loops are very similar.

This is one feature of neural networks models. You can build significantly larger models and train them efficiently with a similar training loop, as long as you have enough computational power.

Bonus points: One challenge in deep learning training is to find the proper hyperparameters. There are many hyperparameters to tune, such as the learning rate, the number of hidden layers, the number of neurons in each layer, the batch size, the number of epochs, etc.

Try to tune the hyperparameters of the convolutional network model to achieve a higher accuracy. For the MNIST dataset, an accuracy of >99% is possible with the LeNet architecture. Could you achieve this?